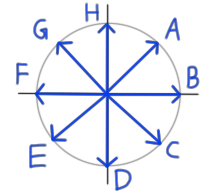
Of the unit vectors $\mathbf{A}$ through $\mathbf{H}$,
- Which have a positive dot product with $\mathbf{A}$?
- Which have a negative dot product with $\mathbf{A}$?
- Which have zero dot product with $\mathbf{A}$?
- Which has the largest dot product with $\mathbf{A}$?
- Which has the most negative dot product with $\mathbf{A}$?