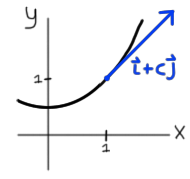
Problem on finding a tangent vector to a curve

$\newcommand{\bfA}{\mathbf{A}}$ $\newcommand{\bfB}{\mathbf{B}}$ $\newcommand{\bfC}{\mathbf{C}}$ $\newcommand{\bfF}{\mathbf{F}}$ $\newcommand{\bfI}{\mathbf{I}}$ $\newcommand{\bfa}{\mathbf{a}}$ $\newcommand{\bfb}{\mathbf{b}}$ $\newcommand{\bfc}{\mathbf{c}}$ $\newcommand{\bfd}{\mathbf{d}}$ $\newcommand{\bfe}{\mathbf{e}}$ $\newcommand{\bfi}{\mathbf{i}}$ $\newcommand{\bfj}{\mathbf{j}}$ $\newcommand{\bfk}{\mathbf{k}}$ $\newcommand{\bfn}{\mathbf{n}}$ $\newcommand{\bfr}{\mathbf{r}}$ $\newcommand{\bfu}{\mathbf{u}}$ $\newcommand{\bfv}{\mathbf{v}}$ $\newcommand{\bfw}{\mathbf{w}}$ $\newcommand{\bfx}{\mathbf{x}}$ $\newcommand{\bfy}{\mathbf{y}}$ $\newcommand{\bfz}{\mathbf{z}}$
Let $y = \frac{1}{2} x^2+\frac{1}{2}$. For what value of $c$ is $\mathbf{i} + c \mathbf{j}$ a tangent vector to $y(x)$ at $x=1$?

  • Solution

    The vector is tangent to the curve if it has the same 'slope' in the $xy$ plane as the tangent line to $y(x)$ at $x=1$.
    Recall that
    The derivative $\frac{dy}{dx}(x)$ gives the slope of the tangent line to $y(x)$ at $x$.
    Computing that $\frac{dy}{dx} = x$, the slope of $y(x)$ at $x=1$ is $1$.
    The 'slope' of the vector is given by its rise of $c$ over its run of $1$:
    Hence, $\frac{c}{1}=1$, and the tangent vector is $\mathbf{i} + \mathbf{j}.$

Related topics