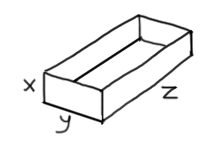
Problem on optimization without constraint

Consider an open box with no top, as shown. The box has volume $32$ and dimensions $x,y,z$. Using the constraint to substitute for $z$, find the dimensions of the box with minimal surface area:

What is the surface area of the box in terms of just $x$ and $y$?
Using (a), find the values of $x$, $y$, $z$ that minimize the box's surface area.

Solution
Part (a) - Surface area in terms of $x$ and $y$
In order to write down an equation for surface area without $z$, we start by writing down a direct expression for surface area: $$\text{Area} = 2 x y + 2 x z + yz$$
Now, we write down the volume constraint and solve for $z$ in terms of $x,y$: $$\begin{align} xyz &= 32 \\ z &= \frac{32}{x y} \tag{1}\end{align}$$
Substituting $z$ into the expression for area, we get $$ A(x,y) = 2 x y + \frac{64}{y} + \frac{32}{x}$$
Part (b) - Finding the minimal surface area
We observe the problem is an unconstrained minimization problem in $x$ and $y$. This is because those variables are free to be any positive numbers. The constraint that the volume is 32 has already been enforced in the expression for $A(x,y)$.
Recall that:
Critical points of functions of several variables

To find the extreme points of a function without constraint, find the critical points by setting all partial derivatives equal to zero.
Partial derivatives

We now compute the partial derivatives of $A(x,y)$: $$\begin{align} \partial_x A(x,y) &= 2y - \frac{32}{x^2} \\ \partial_y A(x,y) &= 2x - \frac{64}{y^2} \end{align}$$
Setting these derivatives to 0 we see that a critical point can only occur at $(x,y)$ satisfying $$\begin{align} 2y-\frac{32}{x^2} &=0 \tag{2}\\ 2x - \frac{64}{y^2} &= 0 \tag{3} \end{align}$$
Solving (2) for $y$ and plugging into (3), we get $x^4 -8x = 0$.
To solve for $x$ we factor: $$x^4 - 8x = x(x^3 - 8) = x(x-2)(x^2 + 2x + 4) =0.$$
This expression is zero if $x=0$ or $x=2$. We ignore the $x=0$ solution because $A$ is undefined for $x=0$. Hence the only critical point is at $x=2$. We can now use (1) and (2) to find that $y=4$ and $z=4$.
We suspect that the minimal surface area is achieved with $$x=2, y=4, z=4.$$
(see details)

We could use the second derivative test to verify that these values indeed provide a minimum.

Problem on optimization without constraint

Solution

Part (a) - Surface area in terms of $x$ and $y$

Part (b) - Finding the minimal surface area

Related topics