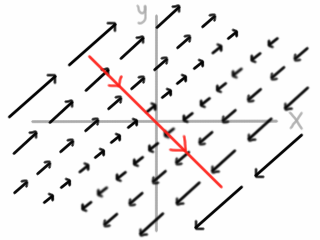
To understand the value of the line integral $\int_C \mathbf{F}\cdot d\mathbf{r}$ without computation, we see whether the integrand, $\mathbf{F}\cdot d\mathbf{r}$, tends to be more positive, more negative, or equally balanced between positive and negative.