Problem on the sign of dot products

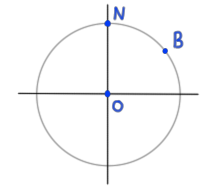
Let $\mathbf{O}, \mathbf{N}, \mathbf{B}$ be three points as shown.
(a) What is the sign of the dot product $(\mathbf{B} - \mathbf{O}) \cdot (\mathbf{N} - \mathbf{O})$?
(b) What is the sign of the dot product $(\mathbf{B} - \mathbf{N}) \cdot (\mathbf{N} - \mathbf{O})$?

Solution
Part (a)
Because we are interested in the dot product of the difference of vectors, we recall the geometric meaning of vector subtraction.
Subtraction gives the vector between two points

The vector from $\mathbf{x}$ to $\mathbf{y}$ is given by $\mathbf{y} - \mathbf{x}$.
Now we draw the vectors $\mathbf{B} - \mathbf{O}$ and $\mathbf{N} - \mathbf{O}$.
Recall that
Dot product angle formula

If $\theta$ is the angle between two vectors $\bfx$ and $\bfy$, $$\mathbf{x} \cdot \mathbf{y} = \left | \mathbf{x} \right | \left | \mathbf{y} \right | \cos \theta$$
Dot product is positive for vectors in the same general direction

The dot product between two vectors is positive if the angle between the vectors is less than $\pi/2$.
From the picture, the vectors appear to be separated by an angle of a little greater than $\pi/4$. Hence the dot product is positive.
Part (b)
We begin by drawing the vectors $\mathbf{B} - \mathbf{N}$ and $\mathbf{N} - \mathbf{O}$ .
The angle between these vectors is greater than $\pi/2$. Hence, $\cos \theta < 0$ and the dot product is negative.

Problem on the sign of dot products

Solution

Part (a)

Part (b)

Related topics