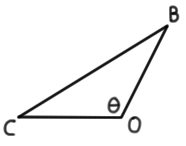
Problem on vectors and the law of cosines

$\newcommand{\bfA}{\mathbf{A}}$ $\newcommand{\bfB}{\mathbf{B}}$ $\newcommand{\bfC}{\mathbf{C}}$ $\newcommand{\bfF}{\mathbf{F}}$ $\newcommand{\bfI}{\mathbf{I}}$ $\newcommand{\bfa}{\mathbf{a}}$ $\newcommand{\bfb}{\mathbf{b}}$ $\newcommand{\bfc}{\mathbf{c}}$ $\newcommand{\bfd}{\mathbf{d}}$ $\newcommand{\bfe}{\mathbf{e}}$ $\newcommand{\bfi}{\mathbf{i}}$ $\newcommand{\bfj}{\mathbf{j}}$ $\newcommand{\bfk}{\mathbf{k}}$ $\newcommand{\bfn}{\mathbf{n}}$ $\newcommand{\bfr}{\mathbf{r}}$ $\newcommand{\bfu}{\mathbf{u}}$ $\newcommand{\bfv}{\mathbf{v}}$ $\newcommand{\bfw}{\mathbf{w}}$ $\newcommand{\bfx}{\mathbf{x}}$ $\newcommand{\bfy}{\mathbf{y}}$ $\newcommand{\bfz}{\mathbf{z}}$
Derive the law of cosines using the dot product:
(a) Write $\text{CB}$ in terms of $\text{OB}$ and $\text{OC}$
(b) Write $\left | \text{CB} \right|^2$ in terms of $\left | \text{OB} \right |$, $\left | \text{OC} \right |$ and $\text{OB} \cdot \text{OC}$
(c) Show that $\left | \text{CB} \right|^2 = \left | \text{OB} \right|^2 + \left | \text{OC} \right |^2 - 2 \left | \text{OB} \right| \left | \text{OC} \right| \cos \theta$.

Related topics