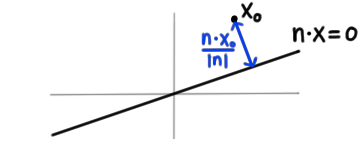Problem on finding the distance from a point to a line

Consider the point $\bfx_0 = (x_0, y_0)$ and the line given by $\bfn \cdot \bfx = 0$, where $\bfn = (a, b)$. Show that the minimum distance from $\bfx_0$ to the line $\bfn\cdot\bfx=0$ is $\frac{\left |\bfn\cdot \bfx_0 \right|}{\left| \bfn \right| }$.

Solution
Recall that
The nearest point on a line can be found by dropping down a line segment perpendicular to the line.
The minimum distance to the line is the length of this line segment.
Visually, this line segment is:
The length of this dropped-down perpendicular segment equals the absolute value of the component of $\bfx_0$ along a vector perpendicular to the line $\bfn\cdot\bfx = 0$:
Component along a vector
Our strategy is to find a perpendicular vector to the line. We then compute the component of $\bfx_0$ along that vector.
Recall that
Dot product of perpendicular vectors is zero

Two vectors are perpendicular if their dot product is zero.
Hence, the line consists of precisely the points that are perpendicular to $\bfn$. That is, $\bfn$ is a normal vector to the line.
Our picture is now:
Recall that
Component along a vector

The component of $\bfx_0$ along $\bfn$ is $\frac{\bfn\cdot \bfx_0}{\left| \bfn \right|}.$
Because the component of $\bfx_0$ along $\bfn$ may be negative, the distance to the line is the absolute value of the component: $$\frac{\left |\bfn\cdot \bfx_0 \right|}{\left| \bfn \right| }.$$

Problem on finding the distance from a point to a line

Solution

Related topics